RNN

1.简单的序列模型

自回归模型

在序列模型中，我们要估计的是$P(x_t|x_{t-1},...,x_1)$，而如果只是用回归(相当于对已有的带有标签的数据做拟合)模型，数据量是很大的，我们采取的模型有两种：

（1）自回归模型autoregressive models

用前面时刻的$x_{t-\lambda},...,x_{t-1}$的线性组合等来得到$x_t$,$\lambda=1$即为一阶自回归模型，$\lambda=2$即为二阶自回归模型。

（2）隐变量自回归模型latent autoregressive models

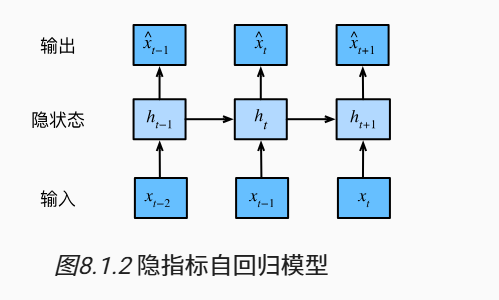
与上文不同的是，上文显式地利用了历史时刻的信息，而隐变量自回归模型保留一些对过去的总结$h_{t-1}$(对t-1时刻之前且包括t-1时刻的过去的总结),基于$P(x_t|h_{t-1})$来计算$x_t$,同时$h_t$显然也是不断更新的，用到动态规划的思想，$h_{t-1}=g(h_{t-2},x_{t-1})$ 如下图

马尔科夫模型与n元语法

一阶马尔科夫模型 $P(x_t|x_{t-1},...,x_1)=P(x_t|x_{t-1})$

将马尔可夫模型应用在语言序列建模上

2.循环神经网络（RNN）

a.为什么需要RNN？

RNN是建立在神经网络基础之上的一种序列模型，我们需要序列模型是因为它能挖掘数据之中的时序或者语义信息。
举个例子：
比如我们要预测在一句话之中词A的下一个词B，要使得词B的加入是合乎语义的。而如果不用序列模型，即用忽视历史时刻的信息，将当前时刻的信息作为输入，得到输出，这样就忽视了词语之间的联系。

b.RNN的原理

(1) 仅仅使用自回归模型

如果我们使用自回归模型，即$x_t$取决于历史时刻的$x_{t-1},...,x_{t-\lambda}$,那么加入我们希望尽可能多的考虑历史时刻的信息，$\lambda$自然就要增大，这样的参数数量便会增加
注：对于参数增加的理解如下

(2) 因而不如使用隐变量模型

$P(x_t|x_{t-1},...,x_1)=P(x_t|h_{t-1})$
$h_t=f(x_t,h_{t-1})$
其中$h_{t-1}$是隐藏变量hidden variable,代表的是截至t时刻之前的序列信息

(3) 具体的RNN网络

假设我们的1个batch有n个序列，在每个序列的时间步t处输入的$x_t$是d维向量，即在batch的时间步t处我们输入的是$X_{n \times d}$矩阵；类似的，$H_t \in \mathbb{R}^{n\times h}$表示时间t的隐藏变量
从而 $H_t=\theta(X_tW_{dh}+H_{t-1}W_{hh}+b_h)$,
而对于每个时间步t，我们都可以得到一个对应的输出$O_t=H_tW_{hq}+b_q$(当然，我们不一定都需要每个时刻的输出。)
$H_t$在每一个时间步的计算都是类似的，是循环的，这也是循环神经网络名字的由来。而神经网络中负责计算$H_t$的这一层称循环层。

注：这仅仅是RNN的一种很简单的计算隐藏向量的方式

然而，回到上文所说的“参数增加”，RNN的参数开销并不大，这是因为RNN的参数包括循环层的参数和输出层的参数等，在不同时间步，这些参数都是一样的，即不同时间步的这些参数并非是独立的。

3.RNN pytorch代码实现